一文说清Transformer
四年前的那个风雨交加的夜晚,谷歌的几位算法专家大声疾呼“你只需要注意力!”(Attention Is All You Need),一声炸雷,大名鼎鼎的Transformer模型诞生了,然后是NLP领域变了天,RNN歇菜了。如今,Transformer又来CV领域“踢馆”了,新闻报道都用上“Transformer又拿下一城...”这样的标题了...
现在的Transformer可谓如日中天,我们也“追追星”,跟进一下和Transformer有关的新动向,这篇文章就是Transformer“本传”。需要说明的是,在我们前面已经用了多篇文章介绍注意力(attention)相关的问题,其中已经包括了对Transformer的讨论,但是之前的文章重点再说注意力的本身,Transformer只是作为注意力机制的一个典型模型而已,从这篇文章开始,我们开启对Transformer的“追星之旅”,厘清Transformer的“前世与今生”。本篇文章即是对已经讨论的有关内容的整合,作为“追星”Transformer的开端。
前传:Transformer来之前,大家都在RNN
Transformer的应用场景是NLP领域的序列翻译,在Transformer产生之前,大家一般都是使用基于循环神经网络(RNN)的编码器-解码器(Encoder-Decoder)结构来完成序列翻译。所谓序列翻译,就是输入一个序列,输出另一个序列,例如汉英翻译即输入的序列是汉语表示的一句话,而输出的序列即为对应的英语表达。2014年,基于深度网络的“序列到序列”(Sequence to Sequence,Seq2Seq)模型逐步成为机器翻译的主流方法。但是由于语言中的词汇在重要性上是有区别的,而原生的Seq2Seq模型对所有词汇“雨露均沾”。因此,到了2015年,注意力机制被添加到Seq2Seq模型中,克服了原生Seq2Seq模型的若干重大问题,大幅提高了机器翻译的质量。随后的序列翻译工作基本上都是以上述工作为基础。我们就从这两个模型说起。
Seq2Seq模型
Seq2Seq模型是一类端到端(end-to-end)的算法框架,通过编码器-解码器架构来实现。该模型的目标是给定一个长度为 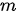 的输入序列
的输入序列 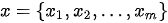 ,期待通过编码器-解码器架构来生成一个长度为
,期待通过编码器-解码器架构来生成一个长度为 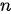 的目标序列
的目标序列 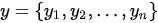 。在机器翻译任务中,
。在机器翻译任务中, 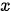 和
和 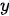 分别代表输入和输出的两个句子。
分别代表输入和输出的两个句子。 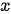 和
和 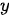 可以是同一种语言(例如
可以是同一种语言(例如 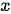 为一篇中文新闻稿,
为一篇中文新闻稿, 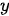 为与之对应的中文摘要),也可以是两种不同的语言(即真正的语言间翻译),而
为与之对应的中文摘要),也可以是两种不同的语言(即真正的语言间翻译),而 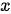 和
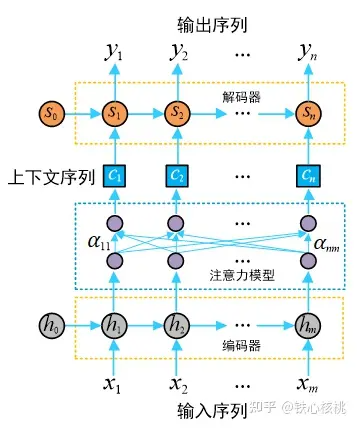
和 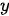 分别由各自的单词序列构成。下图为模型的一个抽象表示,图中的每一个圆圈都表示一个计算单元。
分别由各自的单词序列构成。下图为模型的一个抽象表示,图中的每一个圆圈都表示一个计算单元。
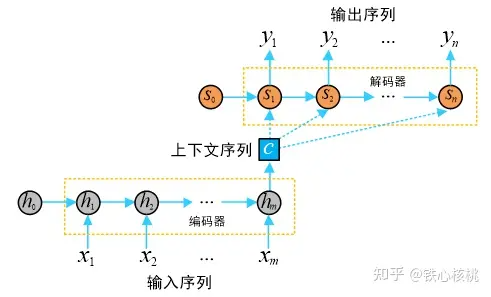
在Seq2Seq模型中,编码器和解码器均以RNN实现(注:在提出Seq2Seq模型的文献中,将编码器和解码器构造为LSTM,在这里不对LSTM和RNN进行区分,事实上Seq2Seq模型中只要求两个网络能够考虑序列中元素的关系即可,况且LSTM本身就是RNN的一个具有门控机制的特例),在上图中其中 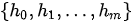 和
和 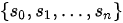 分别为编码器和解码器的隐状态(hidden states)。编码器实现将输入的任意长度的输入序列
分别为编码器和解码器的隐状态(hidden states)。编码器实现将输入的任意长度的输入序列 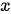 映射为固定长度的上下文序列
映射为固定长度的上下文序列 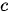 ,该上下文序列为输入序列的一个中间编码表示,表达为
,该上下文序列为输入序列的一个中间编码表示,表达为
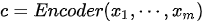
获得 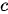 的具体方法有多种,可以取RNN编码器的最后一个隐状态,即
的具体方法有多种,可以取RNN编码器的最后一个隐状态,即 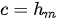 ;也可以是最后一个隐状态的某种变换,即
;也可以是最后一个隐状态的某种变换,即 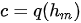 ,还可以对针对所有隐状态做的某种变换,即
,还可以对针对所有隐状态做的某种变换,即 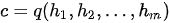 。解码器用来将上述固定长度的中间序列
。解码器用来将上述固定长度的中间序列 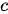 映射为变长度的目标序列作为最终输出
映射为变长度的目标序列作为最终输出 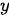 ,其中输出序列中的每一个元素
,其中输出序列中的每一个元素 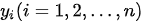 依赖中间序列
依赖中间序列 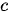 以及其之前的隐状态,即
以及其之前的隐状态,即

Seq2Seq模型可以认为是一个序列到序列转换的通用框架,具有广泛的应用场景,可以完成诸如“中文->英文”的翻译任务,也可以完成“文章->关键词”的摘要提取任务,甚至可以完成“图像->文字”的看图说话任务。
然而,Seq2Seq模型的编码器-解码器架构也存在着明显的缺陷。第一,Seq2Seq模型理论上可以接受任意长度的序列作为输入,但是机器翻译的实践表明,输入的序列越长,模型的翻译质量越差。产生这一问题的原因在于无论输入序列的长短,编码器都会将其映射为一个具有固定长度的上下文序列 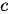 。这就意味着当输入序列的长度过长时,上下文序列将无法表示整个输入序列的信息。试想在一个文本摘要生成的应用中,若
。这就意味着当输入序列的长度过长时,上下文序列将无法表示整个输入序列的信息。试想在一个文本摘要生成的应用中,若 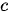 为一个几百维的向量,在针对一段短新闻稿时,也许能够表达新闻稿的全部语义信息,但是面对一篇长篇小说,恐怕其在语义信息表达方面将显得力不从心。第二,在上述编码器-解码器框架中,在生成每一个目标元素
为一个几百维的向量,在针对一段短新闻稿时,也许能够表达新闻稿的全部语义信息,但是面对一篇长篇小说,恐怕其在语义信息表达方面将显得力不从心。第二,在上述编码器-解码器框架中,在生成每一个目标元素 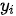 时使用的下文序列
时使用的下文序列 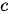 都是相同的,这就意味着输入序列
都是相同的,这就意味着输入序列 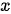 中的每个元素对输出序列
中的每个元素对输出序列 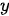 中的每一个元素都具有相同的影响,这种现象是有悖常理的,毕竟在一个输入序列中,不同元素所携带的信息量是不同的,受到关注的程度也自然存在差异。例如在英文到中文的机器翻译应用中,英文语句中的不定冠词“a”或“an”在很多场合是不需要显式翻译的,而类似“very”这样的副词在很多语句中却携带着很重的情感信息。产生上述问题的根本原因就是Seq2Seq模型针对输入序列“不划重点”——即没有应用“注意力”机制。
中的每一个元素都具有相同的影响,这种现象是有悖常理的,毕竟在一个输入序列中,不同元素所携带的信息量是不同的,受到关注的程度也自然存在差异。例如在英文到中文的机器翻译应用中,英文语句中的不定冠词“a”或“an”在很多场合是不需要显式翻译的,而类似“very”这样的副词在很多语句中却携带着很重的情感信息。产生上述问题的根本原因就是Seq2Seq模型针对输入序列“不划重点”——即没有应用“注意力”机制。
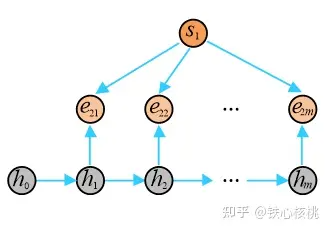
注意力Seq2Seq模型
正是鉴于对不同词汇“划重点”这一问题的考虑,具有注意力机制的Seq2Seq模型(以下简称注意力Seq2Seq模型)在2015年应运而生。与标准Seq2Seq模型相比,注意力模型最大的改进在于其不再要求编码器将输入序列的所有信息都压缩为一个固定长度的上下文序列 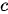 中,取而代之的是将输入序列映射为多个下文序列
中,取而代之的是将输入序列映射为多个下文序列 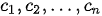 ,其中
,其中 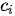 是与输出
是与输出 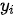 对应的上下文信息(其中
对应的上下文信息(其中 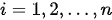 )。在解码器预测输出
)。在解码器预测输出 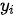 时,其结果依赖与之匹配的上下文序列
时,其结果依赖与之匹配的上下文序列 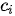 以及其之前的隐状态,即
以及其之前的隐状态,即

下图示意了一个注意力模型的基本结构,其中的注意力模块可以视为是一个具有 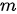 个输入节点和
个输入节点和 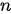 个输出节点的全连接神经网络。
个输出节点的全连接神经网络。
在注意力模型中,每一个上下文序列为编码器所有隐状态向量的加权和
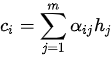
其中 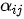 为注意力权重系数(也称为注意力得分)。在编码器中,隐变量
为注意力权重系数(也称为注意力得分)。在编码器中,隐变量 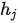 蕴含了输入序列第
蕴含了输入序列第 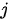 个元素的信息,因此对编码器隐变量按照不同权重求和表示在生成预测结果
个元素的信息,因此对编码器隐变量按照不同权重求和表示在生成预测结果 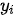 时,对输入序列中的各个元素上分配的注意力是不同的——
时,对输入序列中的各个元素上分配的注意力是不同的—— 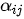 越大,表示第
越大,表示第 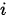 个输出在第
个输出在第 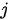 个输入上分配的注意力越多,即生成
个输入上分配的注意力越多,即生成 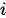 个输出时受到第
个输出时受到第 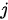 个输入的影响也就越大,反之亦反。
个输入的影响也就越大,反之亦反。
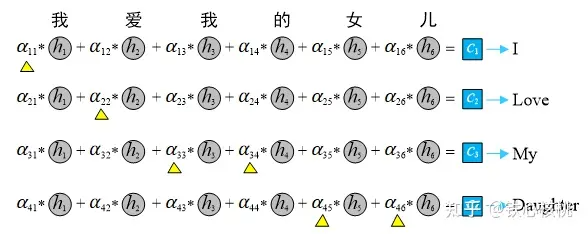
例如,在某个中文到英文的翻译中,输入中文序列为“我爱我的女儿”(我就是个女儿奴,没办法一举例子就是女儿女儿的),则编码器中的隐状态 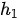 到
到 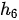 可以分别看作是“我”、“爱”、“我”、“的”、“女”、“儿”这6个字的信息表达。在进行翻译时,注意力的权重变化为
可以分别看作是“我”、“爱”、“我”、“的”、“女”、“儿”这6个字的信息表达。在进行翻译时,注意力的权重变化为
- 与第一个输出
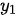 对应的第一个上下文序列
对应的第一个上下文序列 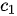 应该将重点放在主语“我”上,因此
应该将重点放在主语“我”上,因此 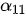 取值较大,而
取值较大,而 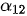 至
至 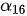 相对较小;
相对较小; - 第二个上下文序列
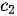 的关注重点为动词“爱”,因此
的关注重点为动词“爱”,因此 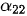 权重占优;
权重占优; - 第三个上下文序列
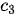 与代表“我”的
与代表“我”的 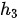 和代表“的”的
和代表“的”的 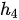 均高度相关,因此
均高度相关,因此 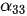 和
和 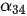 具有较大取值;
具有较大取值; - 最后一个上下文序列
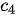 的聚焦点在“女儿”一词上,因此隐状态
的聚焦点在“女儿”一词上,因此隐状态 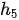 和
和 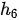 对应的权重
对应的权重 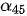 和
和 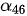 取值相对较大。
取值相对较大。
以上过程可以用下图表示(黄色三角表示取值大的权重系数)。
那么,还剩下最后一个问题,如何得到注意力权重系数 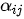 呢?在注意力模型中,注意力权重系数是通过构造一个全连接网络,然后再对该网络输出向量进行概率化得到的。全连接网络的训练与整个模型其他部分的训练同时完成(即实现端到端训练),该网络输出
呢?在注意力模型中,注意力权重系数是通过构造一个全连接网络,然后再对该网络输出向量进行概率化得到的。全连接网络的训练与整个模型其他部分的训练同时完成(即实现端到端训练),该网络输出 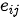 表达了编码器隐状态
表达了编码器隐状态 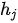 和解码器隐状态
和解码器隐状态 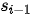 之间的匹配程度,记作
之间的匹配程度,记作 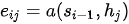 ,其中
,其中 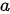 称为对齐模型(alignment model)。下图为以
称为对齐模型(alignment model)。下图为以  为例,对其计算方法的图形化表示。
为例,对其计算方法的图形化表示。
在机器翻译任务中, 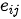 可以视为一种强度表征,表达了输入词的内部表示
可以视为一种强度表征,表达了输入词的内部表示 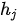 相对上一个输出词的隐状态
相对上一个输出词的隐状态 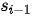 、在决定当词隐状态
、在决定当词隐状态 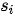 和生成词
和生成词 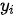 时的重要性。得到
时的重要性。得到 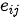 后,对其进行概率化从而进一步得到注意力权重
后,对其进行概率化从而进一步得到注意力权重 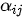 。概率化通过softmax函数来完成,即
。概率化通过softmax函数来完成,即
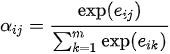
在固定 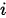 的情况下,有
的情况下,有 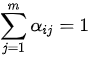 ,即
,即 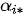 具有概率分布的性质,表达了在决定第
具有概率分布的性质,表达了在决定第 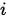 个输出时,注意力在各个输入元素间分布。显然,按照硬性和柔性注意力模型的划分,上述具有注意力机制的Seq2Seq模型属于典型的柔性注意力模型。
个输出时,注意力在各个输入元素间分布。显然,按照硬性和柔性注意力模型的划分,上述具有注意力机制的Seq2Seq模型属于典型的柔性注意力模型。
然而,基于RNN的架构存在着一个明显弊端,那就是RNN属于序列模型,需要以一个接一个的序列化方式进行信息处理,注意力权重需要等待序列全部输入模型之后才能确定,即需要RNN对序列“从头看到尾”。这种架构无论是在训练环节还是推断环节,都具有大量的时间开销,并且难以实现并行处理。例如面对翻译问题“A magazine is stuck in the gun.”,其中的“magazine”到底应该翻译为“杂志”还是“弹匣”?当看到“gun”一词时,将“magazine”翻译为“弹匣”才确认无疑。在基于RNN的机器翻译模型中,需要一步步的顺序处理从magazine到gun的所有词语,而当它们相距较远时RNN中存储的信息将不断被稀释,翻译效果常常难以尽人意,而且效率非常很低。
只要注意力的Transformer
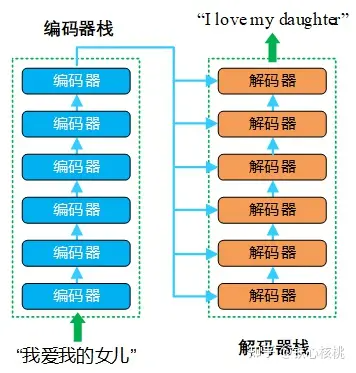
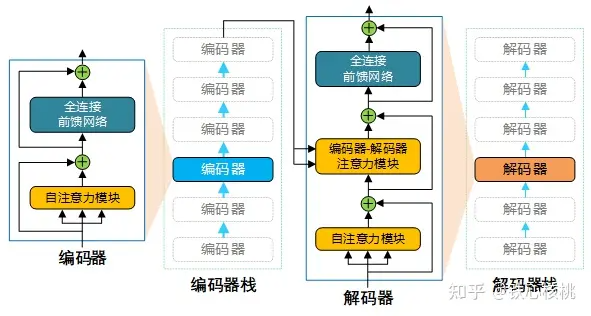
我们不禁要问一个问题:RNN 结构是否真的必要?2017 年,有人针对这个问题给出了的答案——“Attention is all you need”(隐台词是“RNN is unnecessary”)。谷歌大脑、谷歌研究院等团队于 2017 年联合发表文章《Attention Is All You Need》,提出了一种新的注意力 Seq2Seq 模型,以取代之前以 RNN 作为编/解码器实现的 Seq2Seq 模型。该模型一次性的“看见”所有输入的词汇,利用注意力机制将距离不同的单词进行结合。谷歌团队赋予新模型一个大名鼎鼎的名字—“Transformer”,说它“大名鼎鼎”一点也不过分,现如今在 NLP 领域,诸如 BERT(Bidirectional Encoder Representations from Transformers)等诸多有着“逆天”表现的模型都是基于Transformer模型构造的,因此,Transformer模型在现代 NLP领域有着“奠基者”的地位,其重要程度毋庸置疑。谷歌甚至专门开源 Tensor2Tensor(T2T)库,将其作为 Tensorflow 一个新的组成部分,在框架层面实现对Transformer模型的支持。下面就围绕Transformer模型架构和及其使用的注意力机制进行展开讨论。Transformer模型采用的也是编码器-解码器架构,但是在该模型中,编码器和解码器不再是 RNN结构,取而代之的是编码器栈(encoder stack)和解码器栈(decoder stack)(注:所谓的“栈”就是将同一结构重复多次,“stack”翻译为“堆叠”更为合适)。编码器栈和解码器栈中分别为连续 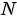 (在 Transformer模型中
(在 Transformer模型中 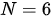 )个具有相同结构的编码器和解码器。下图为Transformer模型的编码器-解码器架构示意图。
)个具有相同结构的编码器和解码器。下图为Transformer模型的编码器-解码器架构示意图。
每一个编码器中又包含两个以串联方式组织的子网络,即:一个自注意力模块(注:这里的自注意力模块具体来说是“Multi-Head Attention”,即“多头注意力”模块,下文将对其进行详细讨论)和一个前馈神经网络。每个子网络都具有残差连接(residual connection),其输出形式为 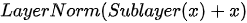 ,其中
,其中 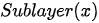 为子网络对输入特征
为子网络对输入特征 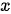 进行的具体映射操作,
进行的具体映射操作, 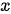 为恒等映射,
为恒等映射, 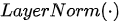 为特征归一化操作。在每个解码器中,除了包含与解码器类似的自注意力模块和全连接前馈网络外,还额外在两个子网络之间添加了另外一个注意力模块(注:该注意力模块称为“编码-解码注意力”模块,同样也是采用多头注意力结构)。与编码器类似,解码器中的三个子网络也均具有残差连接,并且在每个残差合成其后都进行归一化操作。下图示意了Transformer模型中一个编码器和一个解码器的具体结构。
为特征归一化操作。在每个解码器中,除了包含与解码器类似的自注意力模块和全连接前馈网络外,还额外在两个子网络之间添加了另外一个注意力模块(注:该注意力模块称为“编码-解码注意力”模块,同样也是采用多头注意力结构)。与编码器类似,解码器中的三个子网络也均具有残差连接,并且在每个残差合成其后都进行归一化操作。下图示意了Transformer模型中一个编码器和一个解码器的具体结构。
Transformer模型对注意力机制进行了形式化定义:注意力机制可以被描述为一个函数,该函数将一个查询(query,简写为 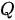 )和一个具有
)和一个具有 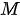 个元素的键-值(key-value,分别简写为
个元素的键-值(key-value,分别简写为 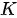 和
和 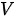 )集合(这个键-值集合也称之为“source”,即“源”)映射为一个值(value)。该函数可以表示为
)集合(这个键-值集合也称之为“source”,即“源”)映射为一个值(value)。该函数可以表示为 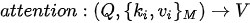 。在具体计算时,注意力的计算分为三个步骤:
。在具体计算时,注意力的计算分为三个步骤:
- 第一步,用输入的
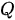 与集合
与集合 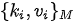 中的每一个
中的每一个 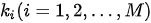 计算相似度,得到
计算相似度,得到 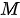 个相似度;
个相似度; - 第二步,通过 softmax 函数将
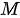 个相似度进行概率化,该步骤会得到一个
个相似度进行概率化,该步骤会得到一个 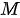 维概率分布;
维概率分布; - 第三步,用概率化后的相似度作为权重系数,对集合
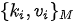 中的
中的 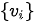 做加权求和,得到最终的输出
做加权求和,得到最终的输出 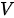 。上述注意力机制的形式化表达为
。上述注意力机制的形式化表达为
![{similarly}(Q,\{k_i,v_i\}_M)=[{similarly}(Q,k_1),\cdots,{similarly}(Q,k_M)]](/resources/upload/aa0a7a970ea7286/1739861319737.png)
![[p_1,\cdots,p_M]={softmax}(Q,\{k_i,v_i\}_M)](/resources/upload/aa0a7a970ea7286/1739861323634.png)
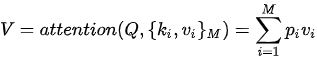
上式中, 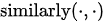 为相似度函数,一种最简单的实现形式即为对输入的两个向量计算点积(dot-product)(注:也可以使用夹角余弦甚至是基于神经网络的相似性度量方法)。从机制上看,注意力机制聚焦的过程体现在权重系数上,权重越大表示投射更多的注意力在对应的值上,即权重代表了信息的重要性。
为相似度函数,一种最简单的实现形式即为对输入的两个向量计算点积(dot-product)(注:也可以使用夹角余弦甚至是基于神经网络的相似性度量方法)。从机制上看,注意力机制聚焦的过程体现在权重系数上,权重越大表示投射更多的注意力在对应的值上,即权重代表了信息的重要性。
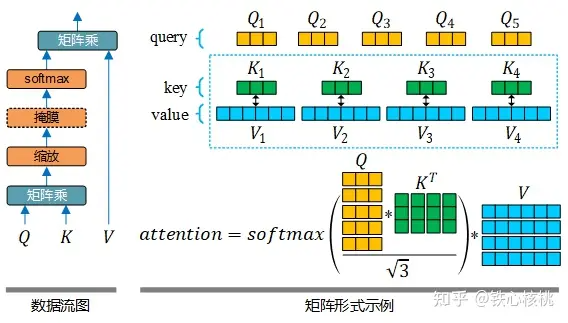
在 Transformer模型中,给出了两种注意力的实现方式:缩放点积注意力(Scaled Dot-Product Attention,SDPA)和多头注意力(Multi-Head Attention,MHA)。其中 SDPA 表示为
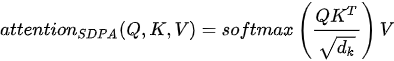
其中 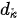 为键(也即查询)的维度,当
为键(也即查询)的维度,当 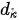 很大时,点积结果将变得非常离散,因此对点积结果除以
很大时,点积结果将变得非常离散,因此对点积结果除以 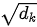 对其进行归一化。在上式中
对其进行归一化。在上式中 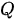 为查询矩阵(多个查询向量拼成的矩阵形式)、
为查询矩阵(多个查询向量拼成的矩阵形式)、 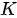 和
和 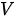 分别为矩阵表示的键和值。下图分别为 SDPA 的数据流图表示和矩阵形式的计算示例(在左图中虚线框所示的掩膜操作为可选操作,只有在解码器中的自注意力模块才会使用)。
分别为矩阵表示的键和值。下图分别为 SDPA 的数据流图表示和矩阵形式的计算示例(在左图中虚线框所示的掩膜操作为可选操作,只有在解码器中的自注意力模块才会使用)。
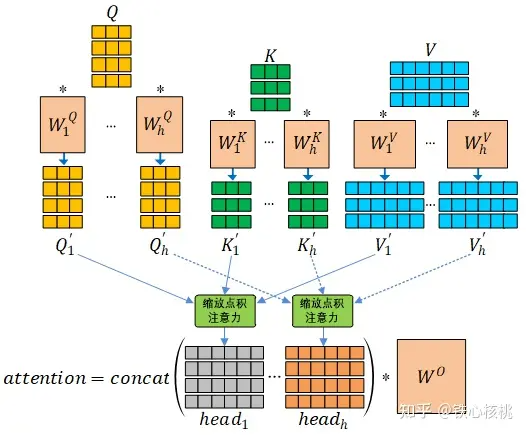
MHA 可以认为是多路融合的 SDPA,其基本操作流程包括多路线性变换、多路 SDPA、多路融合与再次线性变换四个步骤,这四个步骤的形式化表达为
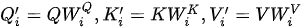
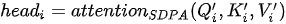
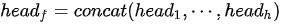
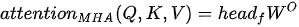
设键(也即查询)和值的向量维度分别为 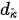 和
和 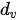 ,设查询矩阵
,设查询矩阵 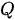 的行数(即查询的条目数)为
的行数(即查询的条目数)为 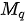 、键矩阵
、键矩阵 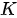 的行数(与值矩阵
的行数(与值矩阵 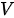 行数相同,即键-值集合的元素个数)为
行数相同,即键-值集合的元素个数)为 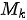 ,则上式中
,则上式中 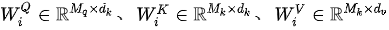 和
和 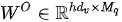 均为可学习线性变换参数;
均为可学习线性变换参数; 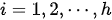 为 MHA 的“头数”(在Transformer模型中设定
为 MHA 的“头数”(在Transformer模型中设定 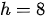 )。下图为 MHA 的矩阵形式计算示例(该例中:
)。下图为 MHA 的矩阵形式计算示例(该例中: 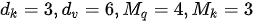 )。
)。
在上述注意力机制的描述中涉及了三个集合:查询集合 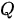 、键集合
、键集合 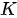 和值集合
和值集合 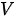 。但是,这些集合并非一定要各不相同,常见情况分为三种:
。但是,这些集合并非一定要各不相同,常见情况分为三种:
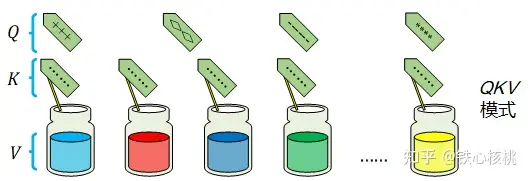
- (A)如果
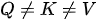 ,即三个集合完全不同(如上面对 SDPA 和 MHA 的示例就是这种情况),我们简称其为
,即三个集合完全不同(如上面对 SDPA 和 MHA 的示例就是这种情况),我们简称其为 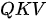 模式;
模式; - (B)如果
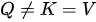 ,即键和值集合是同一个集合,我们简称这种模式为
,即键和值集合是同一个集合,我们简称这种模式为 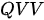 模式;
模式; - (C)如果
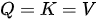 ,即查询、键和值三个集合实际是“一回事儿”,我们将这种模式简称为
,即查询、键和值三个集合实际是“一回事儿”,我们将这种模式简称为 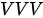 模式。
模式。
在上面的第三种模式中,也正是因为 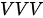 模式下的注意力是以“自嗨”的方式获得的,才将这种模式下的注意力称为“自注意力”(注: 需要强调的是,在 SDPA 结构中,因为注意力是由点积计算得到,故
模式下的注意力是以“自嗨”的方式获得的,才将这种模式下的注意力称为“自注意力”(注: 需要强调的是,在 SDPA 结构中,因为注意力是由点积计算得到,故 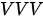 模式意味着 “自己对自己”的注意力权重永远最高。但在
模式意味着 “自己对自己”的注意力权重永远最高。但在 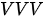 模式在 MHA 结构中则不同,尽管最初只有一份
模式在 MHA 结构中则不同,尽管最初只有一份 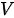 ,但是首先分别需要进行三个线性变换
,但是首先分别需要进行三个线性变换 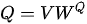 ,
, 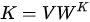 ,
, 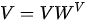 即将手头的
即将手头的 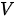 “幻化”出三个版本,分别作为
“幻化”出三个版本,分别作为 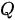 、
、 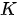 和
和 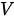 ,这样一来“自己对自己”的注意力权重是高是底就“一切随缘”了)。为了对上述三种模式的注意力机制进行更加充分的说明,下面用一个试剂融合的例子进行类比。
,这样一来“自己对自己”的注意力权重是高是底就“一切随缘”了)。为了对上述三种模式的注意力机制进行更加充分的说明,下面用一个试剂融合的例子进行类比。
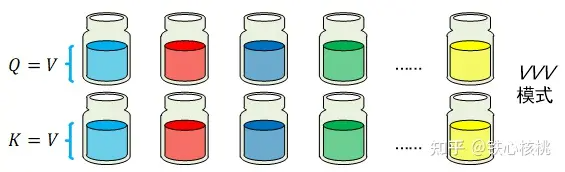
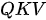 模式:假设有一堆瓶装的纯净试剂,每个瓶子的标签上贴着试剂的品名。因此在这里,试剂本身就是值,而品名对应的就是键。现在有一个品名清单,要依次按照该清单中的品名制作混合试剂(不考虑化学反应),因此在这里,清单上的品名就是查询。混合试剂要用到所有单纯试剂,而且要求某单纯试剂在最终混合试剂中所占的比例由其标签品名与清单品名之间的相似度决定——相似度越高,占的比例也越高。这种模式即
模式:假设有一堆瓶装的纯净试剂,每个瓶子的标签上贴着试剂的品名。因此在这里,试剂本身就是值,而品名对应的就是键。现在有一个品名清单,要依次按照该清单中的品名制作混合试剂(不考虑化学反应),因此在这里,清单上的品名就是查询。混合试剂要用到所有单纯试剂,而且要求某单纯试剂在最终混合试剂中所占的比例由其标签品名与清单品名之间的相似度决定——相似度越高,占的比例也越高。这种模式即 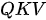 模式。下图为
模式。下图为 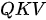 模式下的试剂混合示意。
模式下的试剂混合示意。
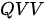 模式:同样还是制作混合试剂的问题,只是现在没有品名清单,只有一些其他类型的少量试剂样本,而且纯净试剂的瓶子上也没有贴标签。现在的任务是选择当前的某一个试剂样本,取不同比例的纯净试剂进行混合,每个纯净试剂的混合比例是按照其与样本试剂之间的相似度决定——试剂本身约相似,占的比例也越高。在这一示例中,样本试剂即是查询,而纯净试剂本身既是键也是值,这种模式即简称为
模式:同样还是制作混合试剂的问题,只是现在没有品名清单,只有一些其他类型的少量试剂样本,而且纯净试剂的瓶子上也没有贴标签。现在的任务是选择当前的某一个试剂样本,取不同比例的纯净试剂进行混合,每个纯净试剂的混合比例是按照其与样本试剂之间的相似度决定——试剂本身约相似,占的比例也越高。在这一示例中,样本试剂即是查询,而纯净试剂本身既是键也是值,这种模式即简称为 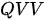 模式。下图为
模式。下图为 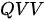 模式下的试剂混合示意。
模式下的试剂混合示意。
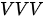 模式:在上面问题的基础上再往前推进一步——标签也好,试剂样本也罢,一概都没有,就只有纯净试剂本身。现在的任务是通过混合纯净试剂的方式得到这些纯净试剂自己,这种模式下的混合比例取决于纯净试剂内部的相似度。这就意味着在此时此刻,每个纯净试剂本身既是键也是值,同时也是查询。下图为
模式:在上面问题的基础上再往前推进一步——标签也好,试剂样本也罢,一概都没有,就只有纯净试剂本身。现在的任务是通过混合纯净试剂的方式得到这些纯净试剂自己,这种模式下的混合比例取决于纯净试剂内部的相似度。这就意味着在此时此刻,每个纯净试剂本身既是键也是值,同时也是查询。下图为  模式下的试剂混合示意。
模式下的试剂混合示意。
上述三种注意力模式中, 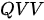 和
和 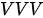 两种模式应用最为广泛,因为二者蕴含了特征表示中的两个非常重要的问题:
两种模式应用最为广泛,因为二者蕴含了特征表示中的两个非常重要的问题: 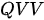 模式代表着如何用一个特征集合表示另一个集合,而
模式代表着如何用一个特征集合表示另一个集合,而 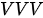 模式代表了如何用一个特征集合表示自己。在Transformer模型中,上述两种模式的注意力机制都有所涉及。
模式代表了如何用一个特征集合表示自己。在Transformer模型中,上述两种模式的注意力机制都有所涉及。
Transformer模型一共有三类注意力模块:编码器自注意力模块(属于 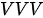 模式)、解码器自注意力模块(属于
模式)、解码器自注意力模块(属于 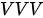 模式)和编码-解码注意力模块(属于
模式)和编码-解码注意力模块(属于 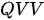 模式)。下面就对其进行讨论。
模式)。下面就对其进行讨论。
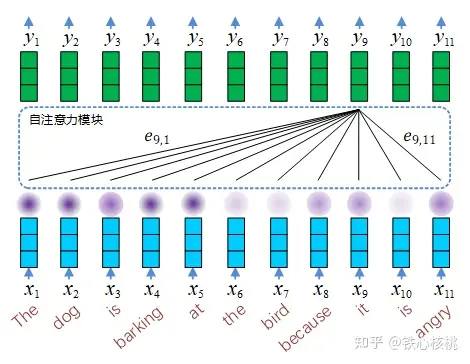
- 编码器自注意力模块
该自注意力模块为 MHA 结构,属于 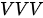 模式,其中
模式,其中 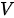 为上一个编码器对输入句子中的每个词的编码(这里的编码可以理解为 RNN 中的隐变量向量,即输入句子中每个词的内部表示。如果是第一个编码器这里的编码即每个词的嵌入向量)。编码器自注意力模块用来捕捉输入句子中词与词之间的关系。例如翻译句子“The dog is barking at the bird because it is angry”,这里的“it”到底说的是狗还是鸟?编码器自注意力模块就是为了在对“it”进行编码时,尽量使得 “dog”对其具有更高的影响力——即注意力权重。下图为针对上述翻译问题的一个自注意力模块示意,其中
为上一个编码器对输入句子中的每个词的编码(这里的编码可以理解为 RNN 中的隐变量向量,即输入句子中每个词的内部表示。如果是第一个编码器这里的编码即每个词的嵌入向量)。编码器自注意力模块用来捕捉输入句子中词与词之间的关系。例如翻译句子“The dog is barking at the bird because it is angry”,这里的“it”到底说的是狗还是鸟?编码器自注意力模块就是为了在对“it”进行编码时,尽量使得 “dog”对其具有更高的影响力——即注意力权重。下图为针对上述翻译问题的一个自注意力模块示意,其中  分别代表句子中每个词的编码(为简化起见不考虑结束符等辅助符号),
分别代表句子中每个词的编码(为简化起见不考虑结束符等辅助符号),  分别为自注意力模块对每个词的输出,
分别为自注意力模块对每个词的输出, 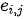 即为自注意力模型输出
即为自注意力模型输出 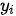 时在输入
时在输入 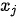 上投射的注意力权重。下图以
上投射的注意力权重。下图以 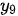 (即针对“it”一词)为例,示意了各个输入编码上的注意力权重分配。
(即针对“it”一词)为例,示意了各个输入编码上的注意力权重分配。
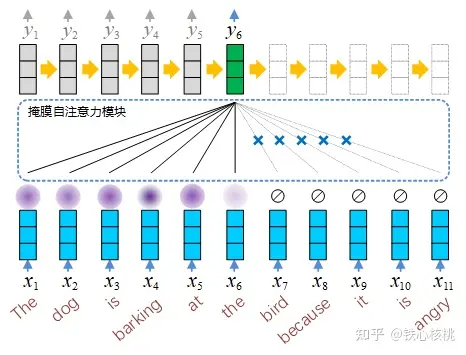
- 解码器自注意力模块
该自注意力模块与编码器自注意力模块的结构非常类似,唯一不同的是添加了掩膜机制,这是由于在解码器中,自注意力模块只被允许处理当前项之前的那些项,这一点与编码器需要“看到”所有项是不同的。上述目标的实现方式非常简单,只要在softmax 注意力权重概率化之前,用掩膜将当前处理项之后的所有项隐去即可,即将注意力的计算改为如下具有掩膜的形式
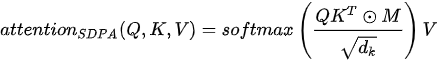
上式中 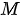 为一个
为一个 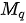 阶下三角矩阵(更一般的,当
阶下三角矩阵(更一般的,当 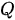 和
和 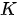 数量不一致时,
数量不一致时, 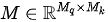 为阶梯型矩阵),其非零元素均为 1,
为阶梯型矩阵),其非零元素均为 1,  表示矩阵的逐元素相乘运算。下图以正在输出
表示矩阵的逐元素相乘运算。下图以正在输出 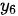 (即针对“the”一词)为例,示意了解码器自注意力模块的执行方式。
(即针对“the”一词)为例,示意了解码器自注意力模块的执行方式。
- 编码-解码注意力模块
在一个解码器中,编码-解码注意力模块位于解码器自注意力模块之后,该模块也被构造为 MHA 结构,但属于 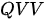 模式。其中
模式。其中 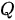 来自于上一个解码器的输出,而
来自于上一个解码器的输出,而 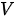 来自于最后一个编码器输出(即也是编码器栈的最终输出)。该注意力模块能够使得解码器中的每个项都能够有重点的“看一遍”输入序列中的每一个词,这一点与基于 RNN结构的 Seq2Seq 结构类似。
来自于最后一个编码器输出(即也是编码器栈的最终输出)。该注意力模块能够使得解码器中的每个项都能够有重点的“看一遍”输入序列中的每一个词,这一点与基于 RNN结构的 Seq2Seq 结构类似。
注意力模块之后是一个前馈神经网络层,该层被构造为逐项操作的全连接网络,针对每个注意力模块得到的输出向量进行独立处理。在相同的层中,每个网络使用相同的参数。在最后一个解码器对特征加工完毕之后,得到的结果随即被送入一个线性变换层和一个softmax 层,其中线性变换层将解码器输出向量的维度变换到字典长度,这一步变换与最开始的词嵌入操作类似。然后该向量由后续的 softmax 层进行概率化,得到的结果即为每个输入词汇在目标词汇上的概率分布。
有了上述概率分布,后面的一切就顺理成章了:在推理阶段,取概率最大位置对应的目标词汇作为最终翻译结果;在训练阶段使用 GT 目标词汇的“独热”编码与上述概率分布构造交叉熵损失函数进行监督训练。
结束语
这篇文章是Transformer系列文章的开篇。在本文中,我们从序列翻译的Seq2Seq模型谈起,介绍了注意力机制在序列翻译中的作用,由此引出并介绍了带有注意力机制的Seq2Seq模型。然后我们步入正题,重点介绍了Transformer模型的结构和注意力机制的作用机理。后续文章我们将开启“追星”模式,去追一追Transformer模型在不同领域的应用现状和研究进展。
